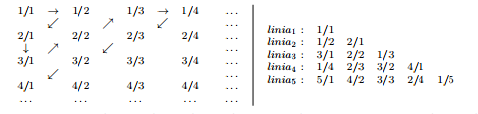Matematicianul Georg Ferdinand Ludwig Philipp Cantor a demonstrat că mulţimea numerelor raţionale este numărabilă, considerând reprezentarea de mai jos-stânga.
Pornind de la această se generează şirul indicat de săgeţi: 1/1, 1/2, 2/1, 3/1, 2/2, 1/3, 1/4, 2/3, 3/2, 4/1, … Pentru un număr n dat (
![]()
) să se determine al n-lea termen din acest şir sub formă nr/num. Programul implementat în C va citi de la consola o serie de m numere (neordonate) şi va scrie termenii corespunzători din şirul descris.
![Rendered by QuickLaTeX.com \[\begin{array}{ccccccccc}1/1 & \rightarrow & 1/2 & & 1/3 & \rightarrow & 1/4 & & \ldots\\& \swarrow & & \nearrow & & \swarrow & & & \ldots\\2/1 & & 2/2 & & 2/3 & & 2/4 & & \ldots\\\downarrow & \nearrow & & \swarrow & & & & &\ldots\\3/1 & & 3/2 & & 3/3 & & 3/4 & & \ldots\\& \swarrow & & & & & & &\ldots\\4/1 & & 4/2 & & 4/3 & & 4/4 & & \ldots\\\ldots & & \ldots & & \ldots & &\ldots & & \ldots\end{array}\]](https://cppc.hpc.pub.ro/wp-content/ql-cache/quicklatex.com-0440669b3fff5e2e9e987abcc670cb01_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc}linia_1: & 1/1 & & & & \\linia_2: & 1/2 & 2/1 & & & \\linia_3: & 3/1 & 2/2 & 1/3 & & \\linia_4: & 1/4 & 2/3 & 3/2 & 4/1 & \\linia_5: & 5/1 & 4/2 & 3/3 & 2/4 & 1/5 \\\end{array}\]](https://cppc.hpc.pub.ro/wp-content/ql-cache/quicklatex.com-d760f51cac782043cbc0bc2154b7521f_l3.png)
Dacă aranjăm elementele şirului pe linii vom obţine reprezentarea de sus-dreapta. Elementele şirului se parcurg apoi în ordine pe linii, de la stânga la dreapta. Un element al şirului poate fi dedus pe baza următoarelor proprietăţi:
- linia i are i elemente,
![Rendered by QuickLaTeX.com \[\forall i \geq 1\]](https://cppc.hpc.pub.ro/wp-content/ql-cache/quicklatex.com-503a628b0c196429605526e561fb7a31_l3.png)
;
- suma
![Rendered by QuickLaTeX.com \[num+nr\]](https://cppc.hpc.pub.ro/wp-content/ql-cache/quicklatex.com-f62cd7066d4a3d2e403bf3d2bcd5a15b_l3.png)
a fiecărui element (
![Rendered by QuickLaTeX.com \[nr/num\]](https://cppc.hpc.pub.ro/wp-content/ql-cache/quicklatex.com-8d3e360babd8fbe4c6af6904df91c011_l3.png)
) de pe linia i este i+1,
![Rendered by QuickLaTeX.com \[\forall i \geq 1\]](https://cppc.hpc.pub.ro/wp-content/ql-cache/quicklatex.com-503a628b0c196429605526e561fb7a31_l3.png)
;
- dacă i este linie pară, primul element este 1/i, numărătorul şi numitorul următoarelor elemente se obţin adunând, respectiv scăzând 1 din numărătorul şi respectiv numitorul elementului precedent;
- dacă i este linie împără, primul element este i/1, numărătorul şi numitorul următoarelor elemente se obţin scăzând, respectiv adunând 1 din numărătorul şi respectiv numitorul elementului precedent.
Exemple: termenul 1 este 1/1; termenul 3.999.999 este 2621/208; termenul 3 este 2/1; termenul 14 este 2/4; termenul 2.000.000 este 1000/1001; termenul 789 este 9/32.