Cerința problemei
Mihai și Ilinca doresc să se apuce de jucat sah, dar deoarece acesta este încă un pic cam complicat pentru ei, și-au ales un joc oarecum asemănător.
Tabla de joc este formata din ![]() căsute. Fiecare căsuță are un cost asociat
căsute. Fiecare căsuță are un cost asociat ![]() , un interval
, un interval ![]() și poate fi colorată în alb sau negru. Jocul este compus din
și poate fi colorată în alb sau negru. Jocul este compus din ![]() ture. La fiecare tură
ture. La fiecare tură ![]() , pentru fiecare casuta
, pentru fiecare casuta![]() se procedează după cum urmează:
se procedează după cum urmează:
– Se caută o căsuță ![]() de culoare opusă căsuței
de culoare opusă căsuței ![]() și se calculează influența acesteia ca fiind
și se calculează influența acesteia ca fiind ![]() . Dintre toate căsuțele
. Dintre toate căsuțele ![]() se alege cea cu influența cea mai mică, și această influență va deveni scorul căsuței
se alege cea cu influența cea mai mică, și această influență va deveni scorul căsuței ![]() , notat cu
, notat cu ![]() .
.
– Dacă ![]() este strict mai mic ca
este strict mai mic ca ![]() , atunci căsuța
, atunci căsuța ![]() își schimbă culoarea (din alb în negru și din negru în alb) și costul acestia se mărește cu
își schimbă culoarea (din alb în negru și din negru în alb) și costul acestia se mărește cu ![]() .
.
-Dacă ![]() este strict mai mare ca
este strict mai mare ca ![]() , atunci căsuța
, atunci căsuța ![]() își schimbă culoarea, costul acesteia se micșorează cu
își schimbă culoarea, costul acesteia se micșorează cu ![]() și se marcheaza faptul că la tura
și se marcheaza faptul că la tura ![]() , căsuța
, căsuța ![]() este subapreciata.
este subapreciata.
La finalul fiecarei ture va trebui sa afișați ![]() numere:
numere:
- Scorul maxim al unei căsuțe albe
- Scorul maxim al unei căsuțe negre
- Numărul de casute negre devenite albe în urma acestei ture
- Numărul de căsuțe albe devenite negre în urma acestei ture.
La finalul celor ![]() ture va trebui sa afișați, pentru fiecare căsuță
ture va trebui sa afișați, pentru fiecare căsuță ![]() , turele la care aceasta a fost subapreciata.
, turele la care aceasta a fost subapreciata.
Structura datelor de intrare și ieșire
Datele de intrare se citesc de la tastatură. Pe prima linie se află ![]() numere întregi,
numere întregi, ![]() ,
, ![]() și
și ![]() , cu semnificația de mai sus.
, cu semnificația de mai sus.
Următoarele ![]() linii au fiecare
linii au fiecare ![]() numere și reprezintă culoarile căsuțelor de joc. Al
numere și reprezintă culoarile căsuțelor de joc. Al ![]() -lea element de pe a
-lea element de pe a ![]() -a linie este
-a linie este ![]() , daca culoarea căsuței
, daca culoarea căsuței ![]() este albă sau
este albă sau ![]() în caz contrar.
în caz contrar.
Următoarele ![]() linii au fiecare
linii au fiecare ![]() numere și reprezintă intervalele căsuțelor de joc. Intervalul căsuței
numere și reprezintă intervalele căsuțelor de joc. Intervalul căsuței ![]() se află pe a
se află pe a ![]() -a dintre aceste linii, fiind format din elementele
-a dintre aceste linii, fiind format din elementele ![]() si
si ![]() .
.
Datele de ieșire trebuie sa conțina ![]() linii, a
linii, a ![]() -a dintre aceste linii având
-a dintre aceste linii având ![]() numere întregi:
numere întregi:
- scorul maxim al unei căsuțe albe
- scorul maxim al unei căsuțe negre
- numărul de casute negre devenite albe în urma turei de joc
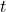 .
. - numărul de căsuțe albe devenite negre în urma turei de joc
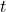 .
.
După acesta urmează ![]() linii ce afișeaza turele la care căsuța
linii ce afișeaza turele la care căsuța ![]() este subapreciată. O linie este formată din indicii căsuței urmată de turele la care căsuța este subapreciată.
este subapreciată. O linie este formată din indicii căsuței urmată de turele la care căsuța este subapreciată.
Restricții şi precizări
* ![]() ≤
≤ ![]() ≤
≤ ![]()
* costurile căsuțelor vor fi numere întergi pozitive, mai mici decât ![]()
* intervalele căsuțelor de joc vor fi numere întregi, cu valoarea absolută mai mica decât ![]() .
.
* limită de timp: problema trebuie să ruleze in mai puțin de ![]()
*Încercați să lucrați cât mai **modularizat**: Faceți-vă funcții pentru calcularea distanței dintre 2 căsuțe, a influenței unei casuțe, al scorului unei căsuțe, etc.
*Folosiți **alocare dinamică** de memorie acolo unde nu se cunoaște dimensiunea unui vector.
Exemplu
- Date de intrare:
2 3 2 0 1 0 1 1 0 2 1 2 2 0 2 1 2 1 3 0 1 0 0 3 4 2 3
Astfel,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Rezultatul rulării problemei pe exemplu ar trebui să fie:
2 3 1 2 2 4 2 1 (0, 0) (0, 1) (0, 2) 0 1 (1, 0) 0 1 (1, 1) (1, 2)
La **prima tură **, scorul căsuțelor este:
2 3 2 3 3 1
După **prima tură**, culorile, respectiv costurile vor fi:
0 1 1 0 1 1
2 1 1 1 0 3
La a **doua tură**, scorul căsuțelor este:
2 3 4 1 2 3
După a **doua tură**, culorile, respectiv costurile vor fi:
0 1 0 1 0 1
2 1 0 0 1 3
Autori: Andrei Pârvu, Emil Racec
Temă 2013